逻辑回归(Logistic Regression)
14 Jun 20171. 摘要
Linear regression 用于解决回归问题。对于分类问题,Logistic regression 就可以施展其才能。和 Linear regression 一样,Logistic regression 也是有监督学习算法(supervised learning)中的一种。
keywords: linear regression, logistic regression, supervised Learning, linear
2. 分类
Logistic regression 和 linear regression 一样,是一种线性机器学习算法,同时也是有监督学习算法。
3. 策略
对于下面的问题,假设样本为(x,y),其真实值\(y\in [0,1]\),y在[0,1] 区间内. 分类算法要么将样本判别为0类,要么判别为1类。
对于这样的分类问题,linear regression 预测函数\(h_{\theta}(x)\)(hypothesis)使用的是线性函数,是无法进行上面的判别的。这时就可使用 logistic regression, 其预测函数使用 logistic function(sigmoid function),如下式所示:
\[h_{\theta}(x)=g({\theta}^T x)=\frac{1}{1+e^{-\theta^Tx}}\]其中 logistic function 就是
\[g(z) = \frac{1}{1+e^{-z}}\]\(\theta^Tx = \theta_0 + \sum_{j=1}^{n}\theta_j x_j\). 符号说明和参考文章-1-线性回归.
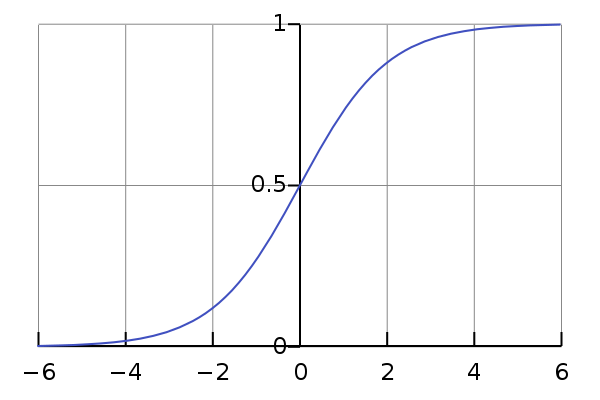
为什么要使用 logistic function?其实也可以使用从0到1至平滑递增的函数。先来看看 logistic function 的导数:
\[\begin{align} g'(z) &= \frac{d}{dz} \frac{1}{1+e^{-z}} \\ &= \frac{1}{(1+e^{-z})^2}(e^{-z}) \\ &= g(z)(1-g(z)) \end{align}\]那么如何求取参数\(\theta\)呢?可通过概率中极大似然估计来计算。
假设,以\(\theta\)为参数,在\(x\)条件下,\(y=0,1\)的概率分别为:
\[\begin{cases} P(y=1|x; \theta) = h_{\theta}(x) \\ P(y=0|x; \theta) = 1-h_{\theta}(x) \end{cases}\]其中,\(x\)是变量,而参数\(\theta\)不是随机变量。
那么概率质量函数(PMF)可表示成:
\(p(y \mid x; \theta) = (h_{\theta}(x))^y(1-h_{\theta}(x))^{1-y}\).
同时再假设m个训练样本是独立生成的,那么参数的似然函数为:
\[\begin{align} L(\theta) &= p(Y \mid X; \theta) \\ &= \prod_{i=1}^{m} p(y^i \mid x^i; \theta) \\ &= \prod_{i=1}^{m} (h_{\theta}(x^i))^{y^i} (1-h_{\theta}(x^i))^{1-y^i} \end{align}\]进行极大似然估计,取对数:
\[\begin{align} l(\theta) &= \log L(\theta) \\ &= \sum_{i=1}^{m} y^i \log h_{\theta}(x^i) + (1-y^i)log(1-h_{\theta}(x^i)) \end{align}\]如何最大化似然函数?
使用 \(\theta := \theta + \alpha \triangledown_{\theta}l(\theta)\)。(此公式和线性回归中使用的不同,因为在线性回归中用极大似然估计时,最大的极大,变为对含参数\(\theta\)的部分取极小值,这样与这里的符号相反。具体可参考文献2-ML-note1)
\[\begin{align} \frac{\partial}{\partial \theta_j} l(\theta) &= \sum_{i=1}^{m} \left[y^i \frac{1}{g(z)}-(1-y^i) \frac{1}{1-g(z)}\right] \frac{d}{dz}g(z) \frac{d}{d\theta_j}z & where \ z=\theta^T x \\ &= \sum_{i=1}^{m} \left[y^i \frac{1}{g(z)}-(1-y^i) \frac{1}{1-g(z)} \right]g(z)(1-g(z))x^i_j \\ &= \sum_{i=1}^{m} \left[ y^i -g(\theta^T x^i) \right]x^i_j \\ &= \sum_{i=1}^{m} \left[ y^i - h_{\theta}(x^i) \right]x^i_j \end{align}\]因此,通过训练样本我们可以更新参数:
\[\theta_j := \theta_j + \alpha \sum_{i=1}^{m} \left[y^j - h_{\theta}(x^i)\right]x^i_j\]这个和 linear regression 中的 LMS update rule 相同。只不过预测函数 hypothesis 不同。
流程
代码
参考
人生苦短, 为欢几何.


